So long, and thanks for all the hamburgers

It’s not true that humanity is committing suicide, as exemplified by the COP28 farce of a climate summit. The world’s industrialists and financiers are committing humanity to ecocide. More than ever, it’s easier to imagine the end of the world than the end of capitalism.

Death by capitalism. That phrase has a certain catchy feeling to it. But it’s no joke, is it? No, no joke at all.

No joke, and no vote. You didn’t get a vote on whether greenhouse gas emissions should continue at a pace to unleash catastrophically rising seas, unbearable heat, droughts, environmental destruction and an increasingly erratic climate in a cascade of cause and effect that will trigger still more climatic instability. The world’s capitalists — in particular, those who control and profit from fossil fuel corporations — have voted, did vote and will continue to vote for profits today and indifference to human and animal life tomorrow. Hurray!

The financial industry mentality has always been to squeeze every dollar out of a stone today and the hell with tomorrow. The fossil fuel industry mentality is much the same. Tomorrow increasingly looks like it will be hell. Tomorrow may not come for a few more decades, perhaps, but it does seem that tomorrow will arrive and it won’t be a pleasant time.

No more than a brief recap of the 28th Conference of the Parties to the United Nations Framework Convention on Climate Change (as COP28 is formally known) is necessary. Destined to be even more of a farce than previous climate change summits given it was hosted by the oil-reliant United Arab Emirates with the chief executive officer of the UAE state oil company, Sultan Al Jaber, serving as COP28 president. Laughter may often be better than crying, but laughter just doesn’t seem right for this level of irresponsibility and contempt for humanity and the environment.

Perhaps next year’s COP29 can be scheduled for the offices of ExxonMobil? Or perhaps the world’s oil majors can bid on which will host? I do know that Baku, Azerbaijan, has been designated as the site for COP29 and that Azerbaijan is a significant oil and gas producer, even if not as big as the United Arab Emirates. But we might as well take the final step toward making these annual climate summits a complete farce. It would at least be more honest.

They delivered empty talk

The official COP28 website is quite cheery and is headlined “We United/We Acted/We Delivered.” Beyond continuing oil and gas profits, it is difficult to say what was delivered. The official final statement declares “the Parties agreed a landmark text named The UAE Consensus, that sets out an ambitious climate agenda to keep 1.5°C within reach. The UAE Consensus calls on Parties to transition away from fossil fuels to reach net zero, encourages them to submit economy-wide Nationally Determined Contributions (NDCs), includes a new specific target to triple renewables and double energy efficiency by 2030, and builds momentum towards a new architecture for climate finance.”

When we look at the details, we find that the “UAE Consensus” is “An unprecedented reference to transitioning away from all fossil fuels to enable the world to reach net zero by 2050” and that “economy-wide emission reduction targets” are “encouraged.” In other words, nothing concrete. What does “transition away” mean? Not much. And that countries are “encouraged” to reduce greenhouse gas emissions means that, as with past climate summits, there are no mechanisms to ensure any promises are kept. And are environmental organizations seen as relevant to any process of reducing emissions? Certainly not! Instead, finance capital will save us: Another point is “Building momentum behind the financial architecture reform agenda, recognizing the role of credit rating agencies for the first time, and calling for a scale up of concessional and grant finance.”

Banks are not going to save us. From 2015, when the Paris Climate Accord was signed, through 2022, 60 of the world’s biggest banks have invested US$4.6 trillion in fossil fuel projects. And the amount of money the controllers of finance capital are investing is growing: $742 billion was invested in the industry in 2021 alone. Four United States-based banks were the worst offenders, according to a report by seven environmental organizations, and three Canadian banks are among the top dozen in the world for financing fossil fuels. Each of these are big contributors to fracking and tar sands production. It’s not only companies like Saudi Aramco and the Abu Dhabi National Oil Company.

What was that about crying or laughing? So it’s more idle talk, the same as previous climate summits. Last year’s COP27 in Egypt established a “loss and damage” fund for Global South countries that remains voluntary and features an implementation plan that “requests” countries that have not yet done so “revisit and strengthen” their 2030 climate targets. Note that word: “requests.” Oh please consider stopping your environmental destruction if it’s not too inconvenient. That was preceded by COP26 in Glasgow failing to enact any enforcement mechanisms; COP25 in Madrid concluding with an announcement of two more years of roundtables; COP24 in Katowice, Poland, promoting coal; and COP23 in Bonn ending with a promise that people will get together and talk some more.

A vague declaration that countries will “transition away” in some unspecified and non-enforceable way is consistent with past climate summits. And what might be expected from a conference in which a record number of fossil fuel delegates were in attendance — more than 2,400 and four times more than were in attendance at COP27. For added fun, the COP28 president, Sultan Al Jaber, declared that a phaseout of fossil fuels would “take the world back into caves” and that there is “no science out there, or no scenario out there, that says that the phase-out of fossil fuel is what’s going to achieve 1.5 [degrees] C.” The OPEC cartel of oil-producing countries declared its members should “proactively reject” any reduction target aimed at fossil fuels and ExxonMobil’s chief executive officer, Darren Woods, complained that climate talks focus too much on renewable energy.

The world was not impressed

Thus it is with less than surprise that independent assessments of COP28 are less than glowing. Here is the assessment of Climate Action Tracker: 

“Few of the sectoral initiatives announced during COP28 will meaningfully contribute to closing the emissions gap. Many of them lack either the ambition, clarity, coverage or accountability needed to really make a difference. We estimate that of the total emissions savings that could be achieved by the pledges, around a quarter is already included in government [nationally determined contributions], around a quarter is additional and achievable, and around half is unlikely to be achieved without further action to improve the initiatives. … The ‘Oil and Gas Decarbonisation Accelerator’ is a prime example of a greenwashing initiative by oil and gas companies. It only focuses on upstream emissions from oil and gas production — but the real change has to come from phasing out fossil fuels, where emissions are at least five times greater.”

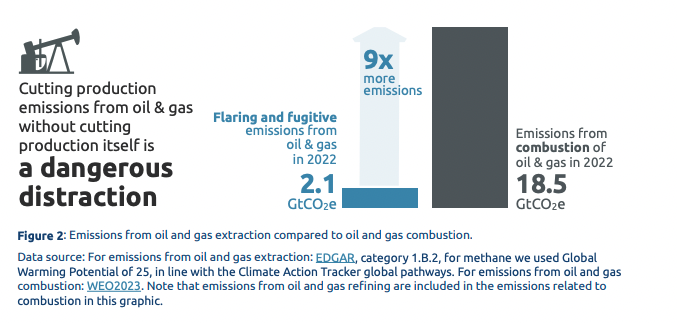
The “Oil and Gas Decarbonisation Accelerator” is a promise by oil companies to reduce emissions that occur during the production of oil and gas, including a halt to “routine flaring” by 2030. Climate Action Tracker’s report states that “The initiative risks being a distraction that misses the woods for the trees.” That is because emissions from the combustion of oil and gas are nearly nine times greater than the emissions from oil and gas extraction. In other words, it is fossil fuels themselves that must be phased out because it is their use that is responsible for the lion’s share of greenhouse gas emissions. But the likelihood of meaningful reduction of production emissions is “negligible” because China and Russia have not signed up to this initiative, while Canada, Norway and the United States “are way behind in meeting their 2030 emissions reduction targets,” and would need to fulfill this promise to make progress on overall reduction pledges.

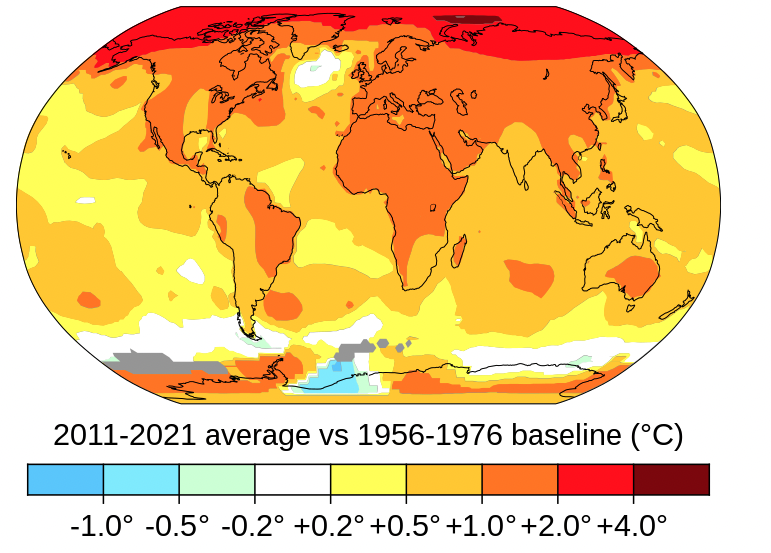
Overall, the world is nowhere near successfully limiting global warming to the Paris Climate Summit goal of holding global warming to 1.5 degrees C. above the pre-industrial level. Even if all current pledges were to be met, a temperature increase of 2.1 degrees by 2100 can be expected, and if current business as usual continues, the world is looking at an increase of 2.7 degrees by the end of the century. And of course if there is no serious mitigation, temperature rises will not stop in 2100.

None of this has gone unnoticed. More than 300 civil society organizations signed a letter calling for a phaseout of fossil fuels as part of an equitable global energy transition. Declaring that “The only way to achieve the ambition of the Paris Agreement is to substantially reduce the extraction and consumption of fossil fuels, starting now,” the letter states:

“COP28 must adopt a comprehensive energy transformation package with legal force – including a full, fast, fair, and funded fossil fuel phaseout, renewable energy and energy efficiency targets, real protections for people and nature, and massively scaled up public funding on fair terms. … By refusing to commit to address the emissions from oil and gas being burned and to end fossil fuel expansion, the proposed ‘Global Decarbonization Accelerator’ would serve as a smokescreen to hide the reality that we need to phase out oil, gas, and coal.”

Will there be enough to eat?

The world’s food supply is at stake in this environmental crisis as well. Representatives of small farmers, such as La Via Campesina, were drowned out by lobbyists for Big Agriculture. Large U.S.-based meat and dairy companies have “spent millions campaigning against climate action and sowing doubt about the links between animal agriculture and climate change,” according to New York University research. Speaking with Inside Climate News, Oliver Lazarus, one of the study’s three authors, said, “These companies are some of the world’s biggest contributors to climate change.” A report in DeSmog notes, “While big meat and dairy corporations have spent millions lobbying against climate action, smallholder farmers are disproportionately victims of the climate crisis.” The DeSmog report added, “While small farms feed most people in low- and middle-income nations, they are responsible for only a fraction of global farming emissions. Helping smallholders to adapt and respond to climate change is fundamental for climate justice.”

The world’s capitalist food system brings us inflation, hunger and waste — more than one-third of the world’s population did not have access to adequate food in 2020, according to a United Nations Food and Agricultural Organization report.

Is it really necessary to restate the case? Another UN study, Emissions Gap Report 2022: The Closing Window, states that climate policies currently in place “point to a 2.8°C temperature rise by the end of the century.” The report adds, “only an urgent system-wide transformation can deliver the enormous cuts needed to limit greenhouse gas emissions by 2030: 45 per cent compared with projections based on policies currently in place to get on track to 1.5°C and 30 per cent for 2°C.”

As a final piling on, there is the Global Tipping Points report issued by a consortium of scientists and issued by Exeter University in Britain. “Harmful tipping points in the natural world pose some of the gravest threats faced by humanity,” the report says. “Their triggering will severely damage our planet’s life-support systems and threaten the stability of our societies.” Five tipping points already at risk of breaching are the Greenland and West Antarctic ice sheets, warm-water coral reefs, North Atlantic Subpolar Gyre circulation and permafrost regions. These would have catastrophic consequences:

“For example, the collapse of the Atlantic Ocean’s great overturning circulation combined with global warming could cause half of the global area for growing wheat and maize to be lost. Five major tipping points are already at risk of being crossed due to warming right now and three more are threatened in the 2030s as the world exceeds 1.5°C global warming. The full damage caused by negative tipping points will be far greater than their initial impact. The effects will cascade through globalised social and economic systems, and could exceed the ability of some countries to adapt. Negative tipping points show that the threat posed by the climate and ecological crisis is far more severe than is commonly understood and is of a magnitude never before faced by humanity.”

Nonetheless, the capitalist system’s industrialists and financiers, and the governments that cater to them and bend to their will, would like nothing more than to continue business as usual. That will soon be impossible. Once again, our descendants — living in a world of flooded cities, food shortages, resource depletion, mass species die-offs, unprecedented human migration and large numbers of people dying should business as usual continue — are not likely to believe that their ruined world would be a fair tradeoff for a handful of industrialists and financiers of the past getting obscenely rich. We live in a global economic system under which it is profitable for a handful of powerful people to profit from the destruction of the environment, and this behavior is richly rewarded. The end of capitalism is precisely what must be envisioned. Organize like your life depends on it, because it does.

COP27 continues the climate summit ritual of words without action

This has become, sadly, a yearly ritual by now. The world’s governments gather together to discuss what should be done about global warming, and finish their time together by issuing statements of concern while doing little concrete to actually solve the problem. And so it is with COP27.

The 27th Conference of the Parties to the United Nations Framework Convention on Climate Change, to use the formal name for COP27, ended with what has the appearance of a breakthrough: An agreement on the establishment of a “loss and damage” fund for Global South countries severely affected by weather and environmental disasters triggered by global warming, and for which they bear almost no responsibility. This finally fulfills a pledge made at the 2009 Climate Summit in Copenhagen. 

Will this fund truly provide compensation to offset the costs borne by underdeveloped countries most at risk from climate upheaval? Given the past records of pledge fulfillment, you may be excused for being skeptical that the fund will come to full fruition, or that sufficient action will be taken to fulfill the goal of previous COPs to cap global warming at 1.5 degrees C. above the pre-industrial level.

On the latter, there is not much time remaining to reverse the ongoing increases in greenhouse gas emissions that continue to be poured into Earth’s atmosphere. According to an analysis published a year ago, Carbon Brief says: 

“In total, humans have pumped around 2,500bn tonnes of CO2 (GtCO2) into the atmosphere since 1850, leaving less than 500GtCO2 of remaining carbon budget to stay below 1.5C of warming. This means that, by the end of 2021, the world will collectively have burned through 86% of the carbon budget for a 50-50 probability of staying below 1.5C, or 89% of the budget for a two-thirds likelihood.”

^{A view from Mount Sinai in Egypt’s Sinai peninsula (photo by Daniel Fafard)}

Despite this looming disaster, the “implementation plan” announced at COP27, “excluded any mention of winding down the use of fossil fuels. It also provided little indication that nations were serious about scaling up efforts to cut emissions,” Carbon Brief reports. 

The implementation plan “requests” countries that have not yet done so “revisit and strengthen” their 2030 climate targets by the end of 2023 so as to to align with the Paris Agreement. 

Maybe if they are asked politely, polluters will stop?

Note that word: “requests.” Oh please consider stopping your environmental destruction if it’s not too inconvenient. Weak-tea wording that is consistent with past COPs. The “we were happy to talk and we will be happy to talk some more” concluding themes of past years wasn’t quite the case this year — the “loss and damage” fund would be a concrete victory should it actually be seriously implemented — but there was no noticeable move to prod the world’s governments, and the polluters and greenhouse-gas emitters they protect, to make it possible to cap global warming at 1.5 degrees. Consider the most recent conference results.

• COP26, held last year in Glasgow, concluded with the world’s governments agreeing to strengthen their greenhouse-gas emission reduction goals, but the commitments were well short of meeting stated goals nor did they have enforcement mechanisms.
• COP25, two years ago in Madrid, ended with a statement that the conference “Notes with concern the state of the global climate system” but limited its action to announcing two more years of roundtables.
• COP24, which featured the host Polish government promoting coal, ended in an agreement to create a rulebook with no real enforcement mechanism to meet greenhouse-gas emission goals that also have no enforcement mechanism.
• COP23 in Bonn ended with a promise that people will get together and talk some more.

Lots of talking and not much doing is, unfortunately, par for the course. Last year saw a strong push to have the COP26 negotiators agree to a “phase out” of coal that was ultimately watered down to a “phase down,” a vague formulation with no specific meaning. Representatives from dozens of countries at COP27 wanted to expand that call to a “phase down” of all fossil fuels, but pushback from Russia and Saudi Arabia and reported foot dragging by the conference’s Egyptian presidency apparently succeeded. There is no such reference to fossil fuels in the conference’s communiqués.

^{Graphic from Carbon Brief}

There was some success in getting the “loss and damage” fund for Global South countries passed, overcoming opposition from the United States and European Union. This was a last-minute triumph for proponents, with the G77 group representing underdeveloped countries and China pushing for the fund to be established. No funding mechanism, however, was agreed to. How much Global North countries will pay and how money will be distributed are to be decided in a series of workshops in 2023. The 2009 agreement that committed developed countries to pay $100 billion per year has never been reached. Some years barely more than half that total was paid and Oxfam argues those reported totals actually overstate what was really delivered.

The official COP27 website is dominated by propaganda, full of baseless articles with titles like “Egypt Climate Champion.” The Egyptian city of Sharm el-Sheikh was the conference host, despite Cairo’s relentless human rights violations and poor environmental record, including repression of environmentalists. The United Nations Climate Change website offers breathless coverage of what it calls a “breakthrough agreement to provide ‘loss and damage’ funding for vulnerable countries hit hard by climate disasters,” but does acknowledge that “a global transformation to a low-carbon economy is expected to require investments” of US$4 trillion to $6 trillion per year, and that “Delivering such funding will require a swift and comprehensive transformation of the financial system and its structures and processes.”

Noting concern, but not matching words with action

Alas, that transformation was not so much as hinted at in the communiqués issued at the conclusion of COP27. Past conferences have ended in a series of statements expressing concern and alarm, but little sense of actually doing something about those concerns and alarms. COP27 has not been an exception. 

The Sharm el-Sheikh Implementation Plan, which functions as the “final communiqué” that had been issued at the conclusion of past conferences, “Underlines the urgent need to address, in a comprehensive and synergetic manner, the interlinked global crises of climate change and biodiversity loss.” Furthermore, the conference “Notes with serious concern the existing gap between current levels of adaptation and levels needed to respond to the adverse effect of climate change” and “Notes with grave concern … the adverse effects of climate change, resulting in devastating economic and non-economic losses.” The conference also “Takes note of the report on the determination of the needs of developing country Parties related to implementing the Convention and the Paris Agreement and in this context urges developed country Parties to provide resources.” 

Is there something other than hand-wringing here? Alas, no. The plan merely “Reiterates its invitation to Parties to consider further actions to reduce by 2030 noncarbon dioxide greenhouse gas emissions, including methane.”

So there remains no enforcement mechanisms or globally agreed standards for any country to meet.

The world’s governments agreed at the Paris Climate Summit in 2015 to hold the global temperature increase to 1.5 degrees Celsius above the pre-Industrial Age average, a change from the previous commitment of 2 degrees. This goal is nowhere near being met. Following last year’s COP26, Climate Action Tracker found that if there were full implementation of submitted and binding long-term targets and 2030 targets, the world’s temperature would increase by 2.1 degrees Celsius from the pre-Industrial Age average. Worse, what the Tracker calls “real world action based on current polices” would result in a temperature increase of 2.7 degrees.

And now? The Tracker, in assessing the latest pledges, this month found that if all current pledges and targets for 2030 and longer-term emissions are met, a temperature rise of 2 degrees C. would be likely be endured by 2100. If only all 2030 emissions targets are met, then a rise of 2.4 degrees is likely. But current trends are for even these inadequate levels to not be met. The “real world action based on current polices” — what is actually currently being done — would see a rise of 2.7 degrees by the end of the 21st century.

“The world is heading for 2.4°C of warming under current 2030 targets. If that number looks familiar, it’s because it is the same as last year,” the Tracker said in its report. “There have been no substantial improvements of existing net zero pledges since COP26. Warming could be 1.8°C, if all targets under discussion are fully implemented, unchanged from last year. Stronger 2030 targets and policy implementation are needed to make these pledges believable and actually provide a reason for optimism.”

Grassroots activists vs. corporate interests

Other environmental organizations are not impressed, either. For example, Sanjay Vashist, the director of Climate Action Network South Asia, had this to say:

“Even as we welcome the announcement of the Loss and Damage funding facility, it is indeed unfortunate that the COP27 failed to deliver on any of the three key outcomes that could have accelerated climate action to avert the worst impacts of the climate crisis. In a year when Pakistan floods reminded the world of the need for urgency, COP 27 had nothing new to offer on ambition to reduce greenhouse gas emissions. At a time when island nations like Sri Lanka are teetering under economic and climate crises, it has failed to find ways to expedite the delivery of promised billion dollars per annum, forget any new or additional financial assistance.”

Asad Rehman, executive director of War on Want and the lead spokesperson for the Climate Justice Coalition, in an interview with Democracy Now, called the conclusion of COP27 “a recipe for disaster.” He said:

“Rich countries have long blocked that idea of an equitable phaseout of fossil fuels. What they’ve wanted to concentrate on is coal, because, largely, developed countries have moved away from coal. And, of course, they’re expanding. I mean, it’s shocking that President Biden, for example, has authorized more permits for expansion of fossil fuels than even Donald Trump did. And, of course, we would widely recognize that President Trump was a climate denialist. So, what we’re seeing is not that kind — not the language that we need in terms of actually a phaseout. Now, what we’ve seen also, of course, because of the pressure of the hundreds of fossil fuel lobbyists and many countries who are relying on fossil fuels for their own economic development, they began to water down their language around fossil fuels.”

Fossil fuel lobbyists attended COP27 in even larger numbers than previous conferences. A report by Corporate Accountability, Corporate Europe Observatory and Global Witness said that 636 fossil fuel lobbyists registered for COP27, an increase of over 25% from COP26. There were more fossil fuel lobbyists than any single national delegation, excepting only the United Arab Emirates. “The extraordinary presence of this industry’s lobbyists at these talks is therefore a twisted joke at the expense of both people and planet,” the report said. 

^{Graphic from Carbon Brief}

The United Arab Emirates, the host for next year’s COP28 meeting, at COP27 promoted oil and gas as a clean source of energy and used the Egypt meeting to promote its state oil company. The UAE also promoted its state oil company’s carbon capture and storage efforts, which even if these could be scaled to its 2030 projection, would “absorb the equivalent of just over two percent of the country’s current overall emissions.” Carbon capture and storage, or sequestration, means “capturing” carbon dioxide before it escapes into the atmosphere and “permanently” storing it underground or underwater, thereby removing it from the air and negating its greenhouse effects. The technology required to achieve this at scale does not exist and has both cost and logistical problems significant enough that sequestration is unlikely to be viable in the foreseeable future. 

That oil and gas interests are unambiguously present and shaping policy is perhaps not surprising because 18 of the 20 companies listed as sponsoring COP27 either directly support or partner with oil and gas companies.

Corporate greenwashing not limited to fossil fuel interests

Fossil fuel companies were not alone in attempting to thwart any progress. The number of registered COP27 delegates who were either directly linked to the world’s largest agribusiness firms or participating in the UN talks as part of delegations that represent industry interests more than doubled from the Glasgow conference. DeSmog reported 160 representatives of Big Agriculture at COP27, compared to 76 at Glasgow last year. Further, “The number of delegates linked to the world’s top five pesticide producers (which between them have 27 lobbyists registered this year), are greater than some country delegations,” DeSmog reports.

“Agribusiness delegates attending the climate talks at the Sharm el-Sheikh resort include the head of a U.S. meat lobby group that until recently claimed the extent of man-made climate change was ‘unknown’, as well as influential trade groups that have lobbied against climate action,” DeSmog said. “The world’s largest meat corporation JBS was also found to have gained privileged access to all negotiations, via the Brazil country delegation.” That is all the more alarming considering the dire situation of the Amazon rainforest, often referred to as the “Earth’s lungs.” The World Wildlife Fund reports that 35% of the Amazon rainforest is either totally lost or highly degraded.

The report says, “The situation has begun to show signs of nearing a point of no return: seasons are changing, surface water is being lost, rivers are becoming increasingly disconnected and polluted, and forests are under immense pressure from increasingly devastating waves of deforestation and fire. This could lead to irreversible change in the near future.” As a further insult, Coca-Cola is one of the sponsors of COP27 despite being called the “world’s leading polluter of plastic in 2021.” Coke has long been connected to human rights abuses in Latin America, as allegations reported in detail by the activist group Killer Coke document.

Human rights violations are nothing new in Egypt. Civil society groups reported surveillance and intimidation at COP27 and the case of Alaa Abd el-Fattah has drawn renewed attention to Cairo’s contempt for human rights. “The rights to freedom of expression and association were severely repressed,” Amnesty International reports in its Egypt report. Arbitrary detention, torture, cruel and inhuman detention, and systematic crackdowns on labor strikes, independent unions and workers expressing grievances or criticism is routine. Why would a conference said to be open to the world’s activists be held in such a country?

What else can be expected when corporate lobbyists swarm climate conferences in such large numbers? When the world’s governments not only make themselves subordinate to multi-national corporations but site the conference in one of the world’s most repressive régimes? The world’s economic system can’t function without endless growth, funnels wealth and therefore power into a minuscule number of hands, causes massive inequality, and forces all to engage in a ruthless competition that requires ever harsher measures to survive. A system designed to deliver massive profits, without regard to social or environmental costs and at the expense of communities and employees. 

We’ll need all the energy and effort that environmental groups can muster if humanity is to have any chance at a livable planet in the future, but it will take more than that. After decades of evidence, it is clear that our environmental and climatic crises can not be solved under capitalism.

Banks fueling global warming is business as usual

The gap between what needs to be done to save the Earth from the environmental disaster of unchecked global warming and what is actually being done continues to widen. Yet another exemplar of this gap is the funding practices of the world’s biggest banks.

Capitalists not concerning themselves with small things like the future ability of the planet to remain livable is nothing new, or we wouldn’t be in our present predicament. But a new report from seven environmental organizations finds that 60 of the world’s biggest banks have invested US$4.6 trillion in fossil fuel projects since the Paris Climate Accord was signed in 2015.

Our descendants, should they be faced with a chaotic climate, massive agricultural disruptions, mass extinctions on land and in the sea, drowned coastal cities and desertification — as they will be should present-day business as usual continue — are not likely to believe that their ruined world will be a fair tradeoff for a handful of industrialists and financiers of the past getting obscenely rich.

Can curses be made retroactive? Perhaps not. But perhaps a worldwide environmental movement can grow sufficiently large and militant to force the necessary changes. There are many out there trying to organize and raise attention — particularly young people, because they will be around long enough to potentially see today’s dire predictions become tomorrow’s reality — but perhaps global warming remains an abstract in too many minds. Or perhaps the daunting challenge of transcending capitalism, without which it is essentially impossible to reverse global warming, is too difficult a challenge. Throwing up our hands in despair would be easier, but if we wish our descendants (or people already alive) to inherit a living world, activism on a world scale is essential.

^{The Alberta tar sands (photo by Howl Arts Collective, Montréal)}

What words should we use to describe an economic system under which it is profitable for a handful of powerful people to profit from the destruction of the environment, and this behavior is richly rewarded?

What words should we use to describe an economic system in which, despite overwhelming evidence of the suicidal course that system is leading humanity, is nonetheless heading straight for global calamity?

What words should we use to those who profit enormously from all this, and why do they have such enormous sums of money to be able to force a continuation of this suicidal course? None of you reading these words voted for this, and none of you can vote to put an end to this. Economic decisions are completely out of the hands of working people; current capitalist ideology has evolved to the point where it is supposed to be unthinkable that economic decisions could be subject to democratic processes. Yet more proof that without economic democracy, there can be no political democracy. A lesson capitalism imposes daily.

Nice words for the environment, gigantic sums of money for fossil fuels

The aforementioned exemplar, a report titled “Banking on Climate Chaos: Financial Fuel Report 2022,” sponsored by Oil Change International, Rainforest Action Network, Indigenous Environmental Network and four other organizations, “finds that even in a year where net-zero commitments were all the rage, the financial sector continued its business-as-usual driving of climate chaos.” Banks are investing in fossil fuels at levels even higher than in 2016, the year after the signing of the Paris Climate Accord, when the world’s governments agreed to the goal of holding the global temperature increase to 1.5 degrees from the pre-industrial level. Of the $4.6 trillion invested by 60 of the world’s biggest banks since the Paris agreement, $742 billion was invested in the industry in 2021 alone.

These banks come from countries around the world, but four United States-based banks were the worst offenders, the report said. “Overall fossil fuel financing remains dominated by four U.S. banks — JPMorgan Chase, Citi, Wells Fargo, and Bank of America — who together account for one quarter of all fossil fuel financing identified over the last six years,” it said. “RBC is Canada’s worst banker of fossil fuels, with Barclays as the worst in Europe and MUFG as the worst in Japan.” Three Canadian banks — RBC (Royal Bank of Canada), Scotiabank and Toronto-Dominion Bank (TD) — are among the top dozen in the world for financing fossil fuels.

Even more alarmingly, Royal Bank of Canada and TD have been the “leaders” in a grotesque expansion of tar sands financing — $23 billion was invested in tar sands production in 2021, a 51 percent increase from 2020. Those two Canadian banks combined doubled their funding for tar sands in 2021 compared to 2016. Even more money was poured into fracking. Last year alone, $62 billion was poured into fracking. Wells Fargo more than doubled its fracking investments to $8 billion in 2021. Since the Paris Climate Accord was signed, four U.S. banks are far and away the biggest culprits in fracking — JPMorgan Chase, Wells Fargo, Citigroup and Bank of America.

^{Graphics via Banking on Climate Chaos report}

Yes, the world’s governments are hypocritical in signing agreements to reduce greenhouse-gas emissions with no enforcement mechanisms and are far from meeting their announced goals. But that certainly is no reason to excuse the financial industry for its significant role in ensuring that more greenhouse gases than ever are thrown into the atmosphere. Or bank hypocrisy. Take London-based Barclays, Europe’s biggest banking contributor to fossil fuel production and the world’s fifth-largest investor in fracking, trailing only the four U.S. banks mentioned just above.

What are we to make of Barclay’s pronouncement, right on its website home page, proclaiming that “Barclays gives shareholders a ‘Say on Climate.’ ” The bank says it will give shareholders “an opportunity to vote on its climate strategy, targets and progress” at its 2022 annual general meeting. Barclays Chairman Nigel Higgins, in a slick pamphlet, claims the bank aims to be “net zero” by 2050. It would seem to be heading in the opposite direction, unless the intention is to pour billions of pounds into fossil fuels until 2049, then magically stop. If the situation weren’t so serious, we could laugh at the chairman’s assertion that “We believe that our original championing of net zero and Paris alignment has made a difference in banking.” If hot air could displace carbon dioxide, I suppose it would make a difference.

The slick pamphlet, 36 pages long, is full of aspirational goals and even goes so far as to proclaim itself a founding member of the Net Zero Banking Alliance, “part of the Glasgow Financial Alliance for Net Zero.” How lovely. The result of last year’s Glasgow climate summit was to continue the tradition of “we were happy to talk and we will be happy to talk some more” while making commitments that ensure global temperatures will soar past 2 degrees C. As for Barclay’s, a reader searches in vain for any mention of what shareholders will be asked to vote on. Those affected by fossil fuel production won’t be asked, of course.

If only hot air could be tapped as an energy source

The intent here isn’t to single out Barclays. Rather, this sort of corporate greenwashing is all too typical. The world’s biggest funder of fossil fuel projects, JPMorgan Chase, for example, claims that it has a “commitment to align key sectors of our financing portfolio with the goals of the Paris Agreement” and “we are measuring the emissions of our clients in key sectors of our financing portfolio.” It would seem there are plenty of greenhouse-gas emissions to measure. But are we supposed to be fooled by this folderol?

Similarly, Royal Bank of Canada, the largest non-U.S. funder of fossil fuels and world’s fifth largest overall funder, says with a straight face that is helping clients reach net-zero goals and is “Setting the standard for best-in-class governance, including through our Climate Strategy & Governance group.” We’d hate to see what a lower standard might look like given the $201 billion it invested in fossil fuels from 2016 to 2021, with 2021’s total double that of 2020.

Although paling in comparison to the US$4.6 trillion the biggest banks have ladled out to the fossil fuel industry over the past five years, including $742 billion in 2021, the World Bank and International Monetary Fund have done their part. The World Bank, funded by the world’s governments, in particular those of the Global North, has provided tens of billions of dollars for fossil fuels since the Paris Climate Accords were signed, reports Urgewald, a non-profit environmental and human rights organization based in Germany. This money includes $12 billion in direct project finance in over 35 countries; as much as $20 billion annually given as government budget support, including for coal projects; and billions more for infrastructure projects that enabled new coal-fired plants that would not have been built otherwise.

The International Monetary Fund (IMF), notorious for imposing extreme austerity on peoples around the world as the price for loans, sometimes imposes additional conditions mandating they “roll out the red carpet for the fossil fuel industry,” reports the U.S.-based environmental organization Friends of the Earth. An FOE report found that:

“Aside from the austerity measures it is so well known for, the IMF has been found to attach conditions in its lending to a number of countries that support new tax breaks for Big Oil. One recent study found that IMF loan programs supported new producer subsidies for coal and gas in Mozambique and Mongolia. The Fund also enabled new legislation in these countries to facilitate public finance of fossil fuel projects. As more countries turn to the IMF for help in coping with COVID-19, it is imperative the IMF does not further entrench fossil fuel dependency around the world. But a recent analysis has found that the IMF’s COVID-19 era loans failed to boost green recovery policies. Another study found that most Covid-19 era loans by the IMF call for austerity measures to be implemented once the pandemic crisis subsides, limiting the resources that countries will have to spend on a just and green recovery.”

Nor can the massive industry subsidies be forgotten. A paper prepared in 2015 by, ironically, four IMF economists, found that subsidies for the fossil fuel industry totaled an astounding $5.6 trillion for 2014. This total included environmental damages, including air pollution, in addition to direct corporate subsidies, below-cost consumer pricing and foregone taxes. No, the IMF was not suddenly questioning capitalism, nor did this report, carefully noting that it did not represent the views of the IMF, devote so much as a single word questioning the economic system that has produced such disastrous outcomes. A more recent IMF study found that fossil fuel subsidies have increased to $5.9 trillion, of which 92 percent arose from undercharging for environmental costs and foregone consumption taxes.

Perhaps those responsible for IMF lending practices don’t read their own organization’s papers (or, if they do, ignore them when they contradict the IMF’s mission of enriching capitalists and immiserating working people). Government officials don’t pay attention to Intergovernmental Panel on Climate Change reports detailing the dire state of the climate. And oil and gas executives laugh at what they get away with and continue to fund “think tanks” that pump out a steady stream of global warming denial. Canada, during the Stephen Harper régime, went so far as to invent the new crime of being a member of an “anti-Canadian petroleum movement,” equating such a stance with terrorism. The Royal Canadian Mounted Police added to this criminalization of advocating for clean air and water by challenging the very idea that human activity is causing global warming or that global warming is even a problem. The basis on which a police force can make such a declaration is unclear.

Capitalism can’t be anything other than what it is

Capitalist governments, not only those countries like Canada and Australia that are dependent on energy and/or mining exports, are beholden to not only the industrialists and financiers who are the real rulers of the world but to the ever intensifying competitive pressures of capitalism, from which industrialists and financiers are not exempt. The controllers of corporations routinely threaten to move elsewhere if political office holders don’t do as corporate executives demand, and the decisions of those executives are not reviewable no matter the effect on the local area.

For corporate executives and the speculators whom they in turn must indulge, maintaining profits means cutting costs (in the first place, the cost of labor), taking bigger shares of existing markets, forcing open new markets and developing new ways of achieving these goals. An enterprise that doesn’t do these gets run out of business by enterprises that do. Larger enterprises, those big enough to be listed on stock markets, have to increase profits, not maintain them, piling on still more pressure — not only from the competition, but from the financial industry, which holds a whip over the producers and distributors of tangible goods and services. A company that merely has steady profits, no matter how high, will be punished by financial speculators because the stock price won’t rise. Stock prices are bets and claims on future profits, and finance capital is relentless in expecting higher stock prices. A corporate executive team that doesn’t deliver will be forced out and replaced by another team that will do as financiers demand.

A corporation can achieve the necessary profits by reducing wages, through either layoffs or moving production to low-wage locations with few regulations. Corporate globalization is due to precisely that. Corporations can also buy machinery so that they can employ less workers; they are doubly incentivized to do this because the machines can be depreciated, lowering their taxes. As more people are put out of work, faster overall economic growth is needed just to maintain existing employment; thus the long-term tendency of more unemployment and lower wages as more people compete for fewer jobs. As industries in national economies become consolidated in an oligarchy of the handful of giant corporations who survived national competition, the route to growth is to expand elsewhere. As the winners in other countries undergo the same process, the relentless competition, now on a planetary scale, winnows these national winners into a small number of global winners.

And when one competitor gives itself a boost to profits (including by finding the country with the lowest wages), the other competitors have to do the same to stay in business. Profits margins decline as the initial boost is eroded by competitors doing the same; and the next round of “innovation” — finding another country with yet lower wages, more layoffs, work speedups, exemptions from environmental rules, pressure on governments to reduce taxes and eliminate tariffs, and inducing governments to enact draconian “free trade” agreements elevating multinational capital above governments — touches off another round of cost cutting and doing whatever possible to boost profits. This is a cycle that has no end under capitalism.

As this mad, endless growth continues, more must be produced, more must be transported, new sources of energy and raw materials must be exploited and more pollution must be dumped into the environment with no cost to the corporate polluter. More carbon dioxide, methane and other greenhouse gases will be thrown into the atmosphere as a direct result of this growth and frenzied activity. Thanks to the massive capital accumulated by the winners of capitalist competition, industrialists and financiers can spend gigantic sums of money spreading propaganda through a network of institutions, bend school and university curricula to their interests, own and control the mass media and buy the political system.

Growth for growth’s sake, and without controls — capitalism is a cancer. A system that nobody controls nor can anybody control it. A system, however, that runs on its own momentum and can’t be anything other than what it is. That we can somehow get control of the machine and make it do good is worse than an illusion.

The future has no value in capitalist economics

Not only is the environment an externality that corporations do not have to account for, thereby dumping the costs on to the public, but orthodox economics doesn’t account for the environment, other than as a source of resources to exploit. The same capitalist market that is nothing more than the aggregate interests of the largest and most powerful industrialists and financiers is supposed to “solve” environmental problems. A May 2009 Monthly Review article by sociologists Richard York, Brett Clark and John Bellamy Foster, “Capitalism in Wonderland,” puts this contradiction in stark perspective:

“Where [orthodox economists] primarily differ is not on their views of the science behind climate change but on their value assumptions about the propriety of shifting burdens to future generations. This lays bare the ideology embedded in orthodox neoclassical economics, a field which regularly presents itself as using objective, even naturalistic, methods for modeling the economy. However, past all of the equations and technical jargon, the dominant economic paradigm is built on a value system that prizes capital accumulation in the short-term, while de-valuing everything else in the present and everything altogether in the future.”

^{A melting glacier (photo by Vojife)}

From that perspective, it follows that present-day environmental damage is of minimal concern to capitalists and future damage of no concern. The industrialists and financiers who reap billions today won’t necessarily be around when the environmental price becomes too high to avoid. The “Capitalism in Wonderland” authors write:

[H]uman life in effect is worth only what each person contributes to the economy as measured in monetary terms. So, if global warming increases mortality in Bangladesh, which it appears likely that it will, this is only reflected in economic models to the extent that the deaths of Bengalis hurt the economy. Since Bangladesh is very poor, [orthodox] economic models … would not estimate it to be worthwhile to prevent deaths there since these losses would show up as minuscule in the measurements. … [E]thical concerns about the intrinsic value of human life and of the lives of other creatures are completely invisible in standard economic models. Increasing human mortality and accelerating the rate of extinctions are to most economists only problems if they undermine the ‘bottom line.’ In other respects they are invisible: as is the natural world as a whole.”

Every incentive is for more

Lest we doubt that orthodox economists are moving down a down a slippery slope in which some humans are valuable and others are without value, recall the infamous memo of Lawrence Summers, written when he was chief economist for the World Bank, in which he wrote:

“I think the economic logic behind dumping a load of toxic waste in the lowest wage country is impeccable and we should face up to that. … The costs of pollution are likely to be non-linear as the initial increments of pollution probably have very low cost. I’ve always thought that under-populated countries in Africa are vastly UNDER-polluted.”

The modern corporation has a legal duty only to provide the maximum profit for its shareholders. In other words, it is expected to act to further its own interest without regard to anything else. The corporation is considered a legal person under U.S. law — one that has no biological limits nor barriers to its growth. Joel Bakan, in the introduction to his book The Corporation: The Pathological Pursuit of Profit and Power, summed up capitalism’s dominant institution this way:

“The corporation’s legally defined mandate is to pursue, relentlessly and without exception, its own self-interest, regardless of the often harmful consequences it might cause to others. As a result, I argue, the corporation is a pathological institution, a dangerous possessor of the great power it wields over people and societies.”

That pathological institution is controlled by, and the wealth produced for, a tiny percentage of people. We can call them the one percent (using the language of Occupy Wall Street), the bourgeoisie (using classical terminology), or industrialists and financiers (using broad labels). Their towering piles of money, hidden away in tax havens and secret bank accounts, are directly built on the backs, the sweat and labor, of their employees. This would be the case even without the added bonus of corporate personhood. Yet no matter how successful today, corporations must expand and be ruthless in beating the competition on pain of going under tomorrow. Every incentive is for more growth, more production, more consumption. Nobody, not even the biggest or most powerful capitalist, has the ability to stop or control it. Even capitalists ride the tiger, although of course they have vastly better ability to manage the vicissitudes of capitalist competition than do working people.

Capitalism is a system that is built, and functions, to generate profit, not to meet needs. If you doubt that, then why are extraordinary amounts of money spent on advertising to get us to buy what we don’t need? If global warming is to be reversed, a rational economic system based on human need, not on private profit, is what is needed. Cooperation for the common good, not competition for the profit of a few at any cost. Is corporate profit really worth the destruction of Earth’s livability?

Another global warming worry: Parts of Earth could become uninhabitable

When we think of the coming disasters of global warming, rising sea levels, disruptions to agriculture and disappearing species come readily to mind. We don’t necessarily think of the livability of the Earth’s surface. But if global warming continues to worsen — and every indication is that will be so — there will be places on Earth that could become uninhabitable.

Uninhabitable in the literal meaning of human beings not being able to survive there.

Such places could come into existence during this century, and perhaps sooner than even climate scientists currently fear, given that lethal combinations of heat and humidity have started to occur for brief periods of time. We are not talking about thinly populated or uninhabited desert locations. We are talking here of cities where tens and hundreds of thousands of people currently live.

Yes, one more reason for humanity to tackle global warming.

To understand why survivability could become impossible in small geographic regions in the foreseeable future and, potentially, much larger regions in the more distant future should current trends in global warming continue, we need to turn to an obscure meteorological measurement known as the “wet-bulb temperature.” This is different from the common air temperature, nor is it the same as the various versions of a “heat index” that provide a “feel like” temperature.

^{Dawes Glacier at the head of Endicott Arm in Alaska (photo by Sean White)}

The wet-bulb temperature is a representation of heat and humidity that measures the impact on the ability of human bodies to cool. A discussion of it by the American Association for the Advancement of Science explains it this way:

“It is so named because it is calculated by wrapping the bulb of a thermometer in a wet cloth. In low humidity, water will evaporate from the cloth, carrying away heat and cooling the thermometer in the same way sweat cools the human body. In these conditions, the wet-bulb temperature will be lower than the air temperature. In high humidity — when the air is more saturated with water vapor — the water cannot evaporate as easily so the cloth stays hot. If the wet cloth cannot cool below the air temperature, neither can human skin.”

Because human skin must be cooler than the body’s core in order for metabolic heat to be conducted to the skin, human skin temperature is strongly regulated at 35 degrees Celsius (95 degrees Fahrenheit). Thus a wet-bulb temperature at that level, should it be sustained, represents the upper limit of what a healthy human being can endure without dying from overheating. It is generally believed that six hours in such conditions, even with steadily drinking fluids and sitting in shade, would be fatal for even the healthiest person, and a sustained wet-bulb temperature a couple of degrees lower would be fatal for many, perhaps most, people.

Simply put, at 35 C/95 F, sweat would not evaporate and our bodies would not be able to regulate our internal temperature.

“When wet-bulb temperatures are extremely high, there is so much moisture in the air that sweating becomes ineffective at removing the body’s excess heat, like what happens in a steam room,” said Colin Raymond, the lead author of a 2020 study on the future habitability of the climate, in an interview published by the U.S. National Oceanic and Atmospheric Administration. “At some point, perhaps after six or more hours, this will lead to organ failure and death in the absence of access to artificial cooling.”

It’s the heat and the humidity

Can a combination of heat and humidity become so intense that a wet-bulb temperature of 35 degrees C (95 degrees F) — the point of effective universal lethality — be reached? Such levels have already been reached in a handful of places, albeit for only one or two hours. Wet-bulb temperatures approaching that lethal level are becoming more common — more than 250 occurrences of 33 degrees C (91 degrees F) have been recorded around the world since 1979.

But such high levels don’t have to be reached for death to occur. “Even at lower wet-bulb temperatures, like 79°F (26°C), those with pre-existing health conditions (like respiratory, cardiovascular, and renal disease), the elderly, as well as those performing strenuous outdoor labor and athletic activities, are at a high risk,” said Radley Horton, a co-author with Dr. Raymond of a 2020 academic study published in Science Advances that examined how high wet-bulb temperatures might get. The 2003 European heat wave caused more than 50,000 deaths at wet-bulb temperatures close to 26 degrees C.

The paper, authored by Dr. Raymond of the Jet Propulsion Laboratory, Dr. Horton of Columbia University and Tom Matthews of Loughborough University, found that “Climate models project the first 35°C [wet-bulb temperature] occurrences by the mid-21st century. However, a comprehensive evaluation of weather station data shows that some coastal subtropical locations have already reported a [wet-bulb temperature] of 35°C and that extreme humid heat overall has more than doubled in frequency since 1979.”

The three climate scientists believe that, under the “business-as-usual RCP8.5 emissions scenario” (a worst-case model in which fossil fuel use continues to increase in a world with ongoing high emissions), wet-bulb temperatures could regularly exceed 35 degrees C in parts of South Asia and the Middle East by the third quarter of the 21st century. They cite three other studies to back up this prediction. They write:

“Our findings indicate that reported occurrences of extreme [wet-bulb temperatures] have increased rapidly at weather stations and in reanalysis data over the last four decades and that parts of the subtropics are very close to the 35°C survivability limit, which has likely already been reached over both sea and land. These trends highlight the magnitude of the changes that have taken place as a result of the global warming to date. At the spatial scale of reanalysis, we project that [wet-bulb temperatures] will regularly exceed 35°C at land grid points with less than 2.5°C of [global] warming since preindustrial—a level that may be reached in the next several decades. According to our weather station analysis, emphasizing land grid points underplays the true risks of extreme [wet-bulb temperatures] along coastlines, which tends to occur when marine air masses are advected even slightly onshore. The southern Persian Gulf shoreline and northern South Asia are home to millions of people, situating them on the front lines of exposure to [wet-bulb temperatures] extremes at the edge of and outside the range of natural variability in which our physiology evolved.”

The limits to the human ability to withstand heat stress

A 2010 study published in PNAS (Proceedings of the National Academy of Sciences) in 2010 by climate scientists Steven C. Sherwood and Matthew Huber warned that the areas that may someday be subject to wet-bulb temperatures are currently inhabited by billions of people, in a worst-case scenario. Dr. Sherwood and Dr. Huber were writing before the Paris Climate Accord, and although the Accord remains inadequate to constrain global warming to 2 degrees C, much less the pact’s 1.5 C goal, it renders the worst-case scenarios less likely. But not impossible, given that a global temperature rise of more than 2 C would set off a cascade of events and feedback loops that are not possible to reasonably forecast.

Even if now somewhat less of a possibility than at the time of their writing, the potential disaster sketched out by Dr. Sherwood and Dr. Huber is frightening. Noting that “heat stress imposes a robust upper limit to adaptation,” they wrote:

“[E]xcedence of 35 °C … would begin to occur with global-mean warming of about 7 °C, calling the habitability of some regions into question. With 11–12 °C warming, such regions would spread to encompass the majority of the human population as currently distributed. Eventual warmings of 12 °C are possible from fossil fuel burning. One implication is that recent estimates of the costs of unmitigated climate change are too low unless the range of possible warming can somehow be narrowed. … If warmings of 10 °C were really to occur in the next three centuries, the area of land likely rendered uninhabitable by heat stress would dwarf that affected by rising sea level. Heat stress thus deserves more attention as a climate-change impact.”

Adding together the Paris Climate Accord goals, if fully implemented, and the efforts by institutions around the world to reduce carbon footprints, it might appear that humanity will avoid the worst-case scenarios. With further effort, those scenarios can be avoided. Nonetheless, it is far too early to breathe a sigh of relief. The emergence of large areas of Earth’s surface that become uninhabitable remains a possibility. The PNAS study said:

“Warming will not stop in 2100 if emissions continue. Each doubling of carbon dioxide is expected to produce 1.9–4.5 °C of warming at equilibrium, but this is poorly constrained on the high side and according to one new estimate has a 5% chance of exceeding 7.1 °C per doubling. Because combustion of all available fossil fuels could produce 2.75 doublings of CO₂ by 2300, even a 4.5 °C sensitivity could eventually produce 12 °C of warming. Degassing of various natural stores of methane and/or CO₂ in a warmer climate could increase warming further. Thus while central estimates of business-as-usual warming by 2100 are 3–4 °C, eventual warmings of 10 °C are quite feasible and even 20 °C is theoretically possible.”

Record heat around the world

The record heat reported around the world in recent months, even if not yet deadly in the absence of sufficiently high humidity, portends trouble. On January 13, the highest temperature ever recorded in the ocean-dominated Southern Hemisphere was reached in Onslow, Western Australia, at 50.7 degrees C (123.3 F). Three stations in Western Australia exceeded 50 degrees C that day; before that week, the entire nation of Australia had recorded only four 50 degree C days in recorded history, according to the Eye on the Storm blog. That same week, multiple stations in Argentina, Brazil and Uruguay neared or beat their all-time high temperatures.

The summer 2021 heat wave in British Columbia, Washington state and Oregon is said by some climate scientists to have been without precedent in meteorological records. The village of Lytton, British Columbia, set an all-time heat record for all of Canada three days in a row and then was destroyed by a wildfire on the fourth day. Portland set its all-time high temperature three days in a row. Seattle reached an all-time high on consecutive days and broke 100 degrees F (37.8 C) three days in a row; there had only been two 100-degree days in its history prior.

^{Lytton, British Columbia, before the wildfire (screen grab from Google maps)}

In his research, Bob Henson, a meteorologist then writing for Weather Underground, reported that 14 examples of 35 degree C wet-bulb readings that have already occurred since 1987 in Pakistan, Saudi Arabia and the United Arab Emirates. Ten of these have occurred since 2000. Six of the 14 occurrences were in one city, Jacobabad, Pakistan; five of these since 2005. Separately, my own study of an interactive map provided by the Columbia University Climate School found six locations where a 35 C/95 F wet-bulb reading had been recorded on at least one occasion. These are Sindh and Khyber Pakhtunkhwa provinces in Pakistan (specific cities not given, but Jacobabad is in Sindh); Hisar, India; Mecca, Saudi Arabia; Ras Al Khaimai, United Arab Emirates; and Yannarie, Western Australia.

There are locations in North America that have approached that level — Palm Springs, California, and multiple locations in Mexico along the Gulf of California have recorded wet-bulb readings of 33 C/91.4 F.

To give an idea of what conditions would achieve a 35 C/95 F wet bulb temperature, these combinations would be required:
• 105 F (40.6 C) & 67% humidity
• 110 F (43.3 C) & 56% humidity
• 115 F (46.1 C) & 46% humidity

Alarm bells continue to get louder, if we want to hear

Unfortunately, the possibility of future areas of uninhabitability isn’t an abstraction or alarmist. Even if all post-Paris promises made at the yearly global climate summits, including last November’s in Glasgow, were fulfilled, global warming would almost certainly go beyond 2 degrees C, and as we have been forced to repeatedly note, there are no enforcement mechanisms to ensure these pledges are met. Following the Glasgow summit (the 26th Conference of the Parties to the United Nations Framework Convention on Climate Change or COP26), Climate Action Tracker reported that full implementation of the goals set for 2030 would be enough for the world’s temperature to rise by 1.9 to 3 degrees by 2100. Worse, what the Tracker calls “real world action based on current polices” would result in a temperature increase of 2 to 3.7 degrees by 2100.

Not that any of this is somehow unknown. The Sixth Assessment Report of the Intergovernmental Panel on Climate Change (IPCC), summarizing the knowledge of the world’s climate scientists, issued last summer, states, “many of the changes observed since the 1950s are unprecedented over decades to millennia. Updated paleoclimate evidence strengthens this assessment; over the past several decades, key indicators of the climate system are increasingly at levels unseen in centuries to millennia and are changing at rates unprecedented in at least the last 2000 years.”

The latest report from IPCC climate scientists, released to the public on February 27, said there is a “very high confidence” that global warming of 1.5 degrees C in the near term “would cause unavoidable increases in multiple climate hazards and present multiple risks to ecosystems and humans.” For the mid to long term (2041 to 2100), there is “high confidence” that “climate change will lead to numerous risks to natural and human systems” and “the magnitude and rate of climate change and associated risks depend strongly on near-term mitigation and adaptation actions.”

There are plenty of other warnings out there. For example, a widely cited 2015 study by the Stockholm Resilience Center, prepared by 18 scientists, found that the Earth is crossing several “planetary boundaries” that together will render the planet much less hospitable. Or that two scientific studies issued in 2015 suggest that so much carbon dioxide already has been thrown into the air that humanity may have already committed itself to a six-meter rise in sea level. Or that the oceans can’t continue to act as shock absorbers — heat accumulated in them is not permanently stored, but can be released back into the atmosphere, potentially providing significant feedback that would accelerate global warming.

Lurking in the background, and not often something that many wish to notice, is the role our world economic system plays in all this. Economic incentives under capitalism are for producing and consuming more, and capitalism can’t function without growth. As has been said so many times, you can’t have infinite growth on a finite planet, and even if taking resources from the rest of the solar system were to become financially viable — something unlikely to happen anytime soon no matter how much we might enjoy watching Star Trek — the solar system is finite as well. We can create a sustainable world economy and society, or nature will impose it on us. And the harshness of the latter will only be magnified by the vast number of refugees that runaway global warming will surely impose. We are part of nature, whether or not we wish to acknowledge that.

COP26: What you’d expect when oil companies are in and environmentalists are out

The annual get-together of the world’s governments, where in most years they express concern about global warming and announce they will continue to talk about it, was not quite the usual washout this year, as small progress was made, at least theoretically. But even if this year’s promises come to fruition, the new round of pledges fall well short of what is needed.

The 26th Conference of the Parties to the United Nations Framework Convention on Climate Change, otherwise known as COP26, concluded its two weeks in Glasgow with congratulations all around for themselves by government participants, as is traditionally the case. If you were to judge by the participants’ pronouncement, you’d think the environment is on the verge of being saved.

For example, the official communiqué issued by the conference loftily declared, “COP26 has today concluded in Glasgow with nearly 200 countries agreeing the Glasgow Climate Pact to keep 1.5C alive and finalise the outstanding elements of the Paris Agreement.” To be fair, there was more acknowledgment that more work needs to be done than is customary, as the communiqué also said, “The Glasgow Climate Pact, combined with increased ambition and action from countries, means that 1.5C remains in sight, but it will only be delivered with concerted and immediate global efforts.”

^{Glasgow at night (photo by Jcdro16)}

But are those very much necessary “concerted and immediate global efforts” going to be undertaken? Ah, details. Another sentence in the communiqué declared, “All countries agreed to revisit and strengthen their current emissions targets to 2030, known as Nationally Determined Contributions (NDCs), in 2022. This will be combined with a yearly political roundtable to consider a global progress report and a Leaders summit in 2023.” We haven’t, alas, dispensed with the “we were happy to talk and we will be happy to talk some more” folderol that has been traditionally offered in lieu of sufficient action.

Consider the most recent conference results. COP25, two years ago in Madrid, ended with a statement that the conference “Notes with concern the state of the global climate system” but limited its action to announcing two more years of roundtables; COP24, which featured the host Polish government promoting coal, ended in an agreement to create a rulebook with no real enforcement mechanism to meet greenhouse-gas emission goals that also have no enforcement mechanism; and COP23 in Bonn ended with a promise that people will get together and talk some more.

They’re “concerned” but not concerned enough to do much about it

It is only proper to acknowledge when progress, however meager, is made, although the bar set by recent conferences is woefully low. Congratulations don’t seem to be in order here. The one tangible accomplishment is that many of the governments representing the world’s biggest contributors to global warming did agree to strengthen their goals to reduce greenhouse-gas emissions. The bad news is that the new commitments remain well short of meeting stated goals. The worse news is that the commitments still have no enforcement mechanisms. Peer pressure appears to remain the preferred methodology, which thus far has not imbued the world’s environmentalists with confidence. For sound reasons.

For example, an effort to have the COP26 negotiators agree to a “phase out” of coal was watered down to a “phase down,” a vague formulation with no specific meaning, and financial transfers from industrialized countries to underdeveloped countries most at risk (which are often the least culpable) have been below what has been promised and well less than what would be sufficient to mitigate damages. Mary Robinson, the former United Nations commissioner for human rights, wrote, “This represents a failure of leadership and a failure of diplomacy. World leaders must be held accountable for the climate disaster playing out on their watch. It is time to call out those who have obstructed the negotiations in Glasgow, and those who continue to downplay the climate emergency.”

^{Marchers for climate justice in Tanzania.}

That would be difficult to argue against, although moral arguments have had limited effect thus far. Unfortunately, the final text from COP26 is full of the “concerns” and “notes” that past conferences have featured. For example, the final text states that it “Expresses alarm and utmost concern that human activities have caused around 1.1 °C of warming to date, that impacts are already being felt in every region, and that carbon budgets consistent with achieving the Paris Agreement temperature goal are now small and being rapidly depleted.” Furthermore, the text “Urges Parties that have not yet communicated new or updated nationally determined contributions to do so as soon as possible” and “Acknowledges the importance of coherent action to respond to the scale of needs caused by the adverse impacts of climate change.”

That will show the atmosphere!

The context here is that the world’s governments agreed at the Paris Climate Summit in 2015 to hold the global temperature increase to 1.5 degrees Celsius above the pre-Industrial Age average, a change from the previous commitment of 2 degrees, although no corresponding pledges were made to reach either goal. Following COP25 two years ago (COP26 was postponed a year due to the Covid-19 pandemic), the pledges then in existence by the world’s governments, were they honored in full, would have allowed global warming to reach 3 degrees, a catastrophic result. This was the conference in which the world’s governments were to have committed themselves to reach the Paris Climate Summit goal.

Temperature goal remains on paper, not in real world

What was actually achieved with the latest round of promises? Climate Action Tracker reports that 123 countries and the European Union submitted new NDC (nationally determined contributions) targets, although a dozen did not strengthen their commitments, a list that includes Australia, Brazil and Russia, each among the world’s biggest contributors of greenhouse gases. An analysis by the Tracker, a collaboration between Climate Analytics and NewClimate Institute, has found that were there to be full implementation of submitted and binding long-term targets and 2030 targets, the world’s temperature would increase by 1.7 to 2.6 degrees Celsius from the pre-Industrial Age average. That is well above the 1.5-degree goal.

Full implementation of just the goals set for 2030 would be enough for the world’s temperature to rise by 1.9 to 3 degrees. Worse, what the Tracker calls “real world action based on current polices” would result in a temperature increase of 2 to 3.7 degrees. The report concludes, “It is clear there is a massive credibility, action and commitment gap that casts a long and dark shadow of doubt over the net zero goals put forward by more than 140 countries, covering 90% of global emissions.” Furthermore:

“Under current policies, we estimate end-of-century warming to be 2.7°C. While this temperature estimate has fallen since our September 2020 assessment, major new policy developments are not the driving factor. We need to see a profound effort in all sectors, in this decade, to decarbonise the world to be in line with 1.5°C. Targets for 2030 remain totally inadequate: the current 2030 targets (without long-term pledges) put us on track for a 2.4°C temperature increase by the end of the century.”

The climate science news site Carbon Brief is not more optimistic. Although dismissing critics who say nothing happened at COP26, Carbon Brief nonetheless said that “current policies will lead to a best-estimate of around 2.6C to 2.7C warming by 2100 (with an uncertainty range of 2C to 3.6C)” and if both conditional and NDCs are met for 2030, the projected warming by 2100 would be 2.4C (1.8C to 3.3C). In the best-case scenario if all long-term net-zero promises are kept, global warming would be held to around 1.8C (1.4C to 2.6C) by 2100, though temperatures would likely peak at close to 2 degrees in mid-21st century before declining.

The above estimates are not set in stone and could prove to be underestimates, Carbon Brief wrote:

“These warming numbers come with some important caveats. First, uncertainties — due to climate sensitivity and carbon cycle feedbacks — are quite large. For example, while current policies are expected to result in around 2.6C to 2.7C warming, the Earth could, in fact, end up with anywhere between 2C to 3.6C or so, depending on how the climate system responds to emissions. These uncertainties are cause for caution and increase the urgency of emissions reductions.”

Despite rhetoric, oil companies welcome but environmentalists aren’t

Corporate influence is never far away when governments attempt to reach policy decisions, and COP26 was no exception. A look at the list of corporate sponsors on the COP26 official website shows at least two natural gas companies and assorted other corporations that would not seem to be appropriate for an environmental summit. Oil companies were also well represented.

DeSmog reports that, although oil companies were not allowed formal roles at COP26, oil majors and state oil companies participated in large numbers as part of business and trade groups or national delegations. “The official participant list is full of executives and employees from the largest publicly traded oil companies in the world, including Royal Dutch Shell and BP,” DeSmog reports. The investigative and research news site adds:

“The presence of oil interests does not stop at the employees and executives from national oil companies and government ministries. Even though the COP26 organizers banned oil companies from sending their own delegations, prominent publicly traded oil majors have found other ways to attend the climate negotiations as well. According to DeSmog’s tally, at least three dozen oil executives gained access to the talks thanks to business and trade associations — and those are only the ones who publicly listed their oil company affiliations. For instance, Royal Dutch Shell sent at least six employees under multiple designations.”

What DeSmog reports is only the tip of the iceberg. Corporate Europe Observatory’s Corporate Accountability campaign reports that more than 100 fossil fuel companies and 30 trade associations were represented at COP26, with so many attending that if the fossil fuel lobby were a country delegation, it would have been the largest. “At least 503 fossil fuel lobbyists, affiliated with some of the world’s biggest polluting oil and gas giants, have been granted access to COP26, flooding the Glasgow conference with corporate influence,” Corporate Accountability reported. Corporate Europe Observatory researcher Pascoe Sabido said:

“COP26 is being sold as the place to raise ambition, but it’s crawling with fossil fuel lobbyists whose only ambition is to stay in business. The likes of Shell and BP are inside these talks despite openly admitting to upping their production of fossil gas. If we’re serious about raising ambition, then fossil fuel lobbyists should be shut out of the talks and out of our national capitals.”

That access is in contrast to environmentalists, who had no such ability to influence negotiations. Mitzi Jonelle Tan, spokesperson for Youth Advocates for Climate Action Philippines, told Democracy Now!:

“It’s funny and ironic, actually, that on the COP26 website, they said they were aiming this to be the most inclusive COP ever, and I think this might have been the most exclusive one. Aside from having all those difficulties and obstacles to actually get to Glasgow, when we get there, COVID was used as an excuse to not let observers come into the important negotiations, yet the fossil fuel industry, the fossil fuel lobbyists, with over 500 delegates, which is more than any other country, was always welcome, was always given the platform, was always given space. And so you can really see that, once again, the U.N. climate summit just prioritized the voices of the privileged and not those that are most affected by the climate crisis.”

Net zero is net unrealism

What efforts that have been made by Global North governments have generally been expressed as goals toward achieving “net zero.” Net zero represents a stabilization in the amount of greenhouse gases in the atmosphere; that is, the amount of greenhouse gases thrown into the atmosphere is balanced by the amount of greenhouse gases that are removed from the atmosphere. The year 2050 is the most common date for countries to say they will achieve net zero, although some countries have pledged to reach that one or two decades later. Of the three largest contributors to greenhouse gases, the European Union and United States have 2050 pledges and China’s goal is “before 2060.”

Are these goals achievable, and, if so, will they be sufficient? This is an important question as the EU, the U.S. and China together account for 46 percent of the world’s greenhouse-gas emissions — more than 16 times the contributions of the 100 least-contributing countries. Climate Action Tracker rates EU and U.S. efforts as “insufficient” and China’s efforts as “highly insufficient.” This rating system “evaluates a broad spectrum of government targets and actions to reduce greenhouse gas emissions in line with the Paris Agreement temperature limit.”

No country is rated as compatible with the Paris Agreement, and only eight countries are rated as “almost sufficient.” Britain is the lone industrial country to receive this designation; the others are Costa Rica, Ethiopia, Kenya, Morocco, Nepal, Nigeria and The Gambia. (The worst category, “critically insufficient,” includes Iran, Russia and Turkey.)

Most of the world is far from achieving net zero. But would doing so truly avoid global catastrophe? Perhaps not. Net zero aspirations are based on the hope that forests and farmlands will pull enough carbon dioxide out of the air to offset the remaining greenhouse-gas production that would still be occurring. Two environmental research scientists, Doreen Stabinsky at the College of the Atlantic and Kate Dooley of the University of Melbourne, throw cold water on this escape hatch. Simply put, too much is being asked of nature.

“Since the world does not yet have technologies capable of removing carbon dioxide from air at any climate-relevant scale, that means relying on nature for carbon dioxide removal,” the two write. The idea that machines will be able to pull huge amounts of carbon dioxide out of the air remains in the realm of fantasy. Carbon dioxide remains in the atmosphere for hundreds to thousands of years; CO₂ must be removed through some means, natural or technological, to have any hope of achieving net zero. As to the potential for the natural world to remove 5 gigatons per year of carbon dioxide from the atmosphere, as some optimistic forecasts hope for, Dr Stabinsky and Dr. Dooley write:

“Reaching the point at which nature can remove 5 gigatons of carbon dioxide each year would take time. And there’s another problem: High levels of removal might last for only a decade or so. When growing trees and restoring ecosystems, the storage potential develops to a peak over decades. While this continues, it reduces over time as ecosystems become saturated, meaning large-scale carbon dioxide removal by natural ecosystems is a one-off opportunity to restore lost carbon stocks. Carbon stored in the terrestrial biosphere — in forests and other ecosystems — doesn’t stay there forever, either. Trees and plants die, sometimes as a result of climate-related wildfires, droughts and warming, and fields are tilled and release carbon.”

If you can’t remove it, you shouldn’t produce it

The two scientists write that ecosystem restoration has the potential to reduce global average temperature by approximately 0.12 degrees C, but such a decline would not occur in time to offset the warming expected within the next two decades. Net zero strategies that rely on temporary removals to balance permanent emissions will fail. There is no alternative to drastically reducing greenhouse-gas emissions. The unreality of net zero pledges put forth by oil companies is laid bare by Dr. Stabinsky and Dr. Dooley:

“ActionAid reviewed the oil major Shell’s net-zero strategy and found that it includes offsetting 120 million tons of carbon dioxide per year through planting forests, estimated to require around 29.5 million acres (12 million hectares) of land. That’s roughly 45,000 square miles. Oxfam reviewed the net-zero pledges for Shell and three other oil and gas producers — BP, TotalEnergies and ENI — and concluded that ‘their plans alone could require an area of land twice the size of the U.K. If the oil and gas sector as a whole adopted similar net zero targets, it could end up requiring land that is nearly half the size of the United States, or one-third of the world’s farmland.’ These numbers provide insight into how these companies, and perhaps many others, view net-zero.”

Not realistic, to put it mildly, given that reforestation at such scales would require removal of a significant portion of the world’s farms. And on top of that, there is no universally accepted definition of what constitutes net zero. Governments can set their own metrics — yet another area of no real accountability — and we also have to think about methane, which although found in far lesser amounts in the atmosphere than carbon dioxide is nonetheless a far more potent contributor to global warming on a molecule-to-molecule basis. Jeff Mackler, writing in CounterPunch, put this together:

“U.N. Secretary-General, Antonio Guterres, has called for a clearer definition of net zero. ‘There is a deficit of credibility and a surplus of confusion over emissions reductions and net zero targets,’ he said, ‘with different meanings and different metrics.’ Indeed, each polluting nation employs its own ‘metrics,’ including positive and hyped deductions for the ‘natural capacity’ of its land mass to absorb carbon dioxide while omitting from its calculations negative factors like deforestation, not to mention the myriad of escaping methane from appliances, fracking and always leaking supermarket refrigeration facilities around the world. Methane’s global warming intensity exceeds CO2 by a factor of 80! Biden’s methane reduction pledge flies in the face of the fact that the U.S. stands first in the world in natural gas fracking, the chief poisonous polluting [byproduct] of which is methane.”

The chimera of carbon trading to achieve an illusory net zero

Unfortunately, the above does not exhaust the list of issues with net zero. Some national net zero goals will be met, in part, through “carbon trading.” One of the agreements reached at COP26 was a deal that permits countries to buy offset credits representing emission cuts by others, which will then be used by the buyers to “achieve” climate targets.

A tax on such offsets, intended to fund climate adaptation in poorer nations and advocated by them, will not be included. According to a Reuters report, “The deal suggests developing nations capitulated to rich nations demands, including the United States, which had objected [to] the levy.” That the carbon trading scheme is being hailed by Brazil’s extreme Right, anti-environment government, is more than enough to question it. The Reuters report said, “The deal was ‘a Brazilian victory’ and the country is gearing up to become a ‘big exporter’ of carbon credits, its environment ministry said on social media. … ‘It should spur investment and the development of projects that could deliver significant emissions reductions,’ Brazil’s chief negotiator Leonardo Cleaver de Athayde told Reuters.”

^{Terminus of Kangerlugssuup Sermerssua glacier in west Greenland (photo by Denis Felikson, via NASA)}

The carbon trading deal, codifying Article 6 of the Paris Agreement after six years of negotiation, does have mechanisms to largely eliminate the double counting that countries like Brazil had previously wanted but does not appear to completely eliminate such practices. But even without double counting, using markets will make it less likely that net zero will be reached in reality rather than only on paper. A report by the Center for International Environmental Law notes, “[C]ountries that aim to meet a significant portion of their [2030 emissions targets] through such offsets — and about half of all countries that submitted [2030 emissions targets] by 2018 indicated an intent to participate in the markets — are less likely to pursue deep decarbonization swiftly than those that focus on domestic cuts. And those countries with a financial interest in exceeding their self-determined contributions, to sell ‘excess’ reductions, are less likely to set ambitious targets.”

To put it in stronger terms, Sebastien Duyck, a senior attorney at the Center, said, “Net zero is a scam. It is used as a smokescreen to avoid actual transition away from fossil fuels and carry on business as usual by relying on unproven carbon capture technologies and offsets. … Article 6 creates a way for public and private investors to weaponize the Paris agreement for the sake of profits at the cost of local communities and indigenous people’s rights.”

So why are fossil fuels subsidized to astonishing amounts? These subsidies are not trivial: A 2015 paper by four economists published by, of all places, the International Monetary Fund estimated the amount of subsidies thrown at the fossil fuel industry as US$5.6 trillion per year. Trillions! That total includes environmental costs in addition to direct corporate subsidies and below-cost consumer pricing. Some — only some — of the damage from these massive subsidies are premature deaths through local air pollution; exacerbating congestion and other adverse side effects of vehicle use; crowding out potentially productive public spending on health, education and infrastructure; discouraging needed investments in energy efficiency, renewables and energy infrastructure; and increasing the vulnerability of countries to volatile international energy prices.

Capitalism is not only cooking the planet to the point where portions of our planet will become uninhabitable and massive disruption to agriculture is certain, but the leading causes of the problem are lavishly subsidized. Who could dream up such a death-wish scenario? Yet here we are. As long as we live under capitalism, incentives will be for more growth, more energy usage, more waste, more accumulation, more inequality, and that inequality will make the struggle for environmental justice and to reverse global warming ever more strenuous. It is simply impossible to decouple the world economic system from the looming environmental catastrophe. The two go together.

Are we up to creating the massive global movement that is the only mechanism that can save the world? If not, our descendants are not likely to believe short-term profits for a few now will be a fair exchange for an unlivable planet for the many then.

Earth burns and the capitalist world talks

Yes, the time for talk is well past and one more report isn’t likely to change minds or induce new action. Nonetheless, it is always useful to have the latest information when dealing with an ongoing emergency. The world’s governments shouldn’t need the latest United Nations report on the state of Earth’s climate to act but if some do care to pay proper attention, the situation is ever more dire.

Officially, the paper under discussion is the Sixth Assessment Report of the Intergovernmental Panel on Climate Change, summarizing the knowledge of the world’s climate scientists. The technical summary of the report spans 150 pages, and that is what we’ll be quoting from. The report is intended “to provide policymakers with regular scientific assessments on climate change, its implications and potential future risks, as well as to put forward adaptation and mitigation options.”

Having paid little more than lip service to past reports, and the ongoing avalanche of scientific papers and the accelerating pace of weather disasters, the world’s governments, beholden as they are to the planet’s industrialists and financiers, aren’t likely to suddenly spring into serious action should office holders bother to read the memos their assistants who might have actually read one of the summaries have sent along.

I wish I could be more optimistic, but consider the recent evidence. At the last gathering of the world’s governments to tackle the issue, the 25th Conference of the Parties to the United Nations Framework Convention on Climate Change in December 2019 in Madrid, otherwise known as COP25, the conference ended with participants announcing the conference “Notes with concern the state of the global climate system” and agreed there would be more opportunities to talk at the next two annual conferences. (Last year’s conference was put off a year and will be held in November in Glasgow.)

^{Graphic credit: NASA, slight adjustments by Femke Nijsse for accessibility.}

The previous year’s COP 24, in Katowice, Poland (the host country’s pavilion featured displays of everyday items such as walls and soap made from coal, for added irony), the conference ended with an agreement to create a rulebook with no real enforcement mechanism. The world’s governments had previously agreed to set goals for reducing their productions of greenhouse gases but to do so on a voluntary basis with no enforcement mechanism, and now those agreements will have guidelines as to how those goals will be reported that also have no enforcement mechanism. And governments will be allowed to use their own methodologies to calculate their progress, a gaping loophole sure to be used to cook the books.

And so it goes, as Kurt Vonnegut was fond of saying. Or perhaps he wasn’t so fond. No matter, the current state of the world’s climate really isn’t a fun topic nowadays. Let’s take a look anyway.

Well on our way to reaching temperature limit

Among the, if you’ll excuse the expression, highlights of the Intergovernmental Panel on Climate Change (IPCC) paper are that the increase in global surface temperature is more than two-thirds of the way toward the 1.5-degree C. limit set by the Paris Accord, the 2015 agreement to reduce greenhouse-gas emissions. Specifically, the IPCC paper states, “For the decade 2011–2020, the increase in global surface temperature since 1850–1900 is assessed to be 1.09 [0.95 to 1.20] °C.” Further, “many of the changes observed since the 1950s are unprecedented over decades to millennia. Updated paleoclimate evidence strengthens this assessment; over the past several decades, key indicators of the climate system are increasingly at levels unseen in centuries to millennia and are changing at rates unprecedented in at least the last 2000 years.”

The report says, “human influence is the principal driver of many changes observed across the atmosphere, ocean, cryosphere and biosphere. … [I]t is now an established fact that human-induced greenhouse gas emissions have led to an increased frequency and/or intensity of some weather and climate extremes since 1850, in particular for temperature extremes.”

^{Terminus of Kangerlugssuup Sermerssua glacier in west Greenland (photo by Denis Felikson, via NASA)}

If an increase since the early years of the Industrial Revolution of 1.5 degrees is a breaking point, how long do we have until that threshold is breached under business as usual? The report says, “combining the larger estimate of global warming to date and the assessed climate response to all considered scenarios, the central estimate of crossing 1.5°C of global warming (for a 20-year period) occurs in the early 2030s, ten years earlier than the midpoint of the likely range assessed in [a 2018 IPCC special report], assuming no major volcanic eruption.” A decade from now!

And that’s not all. The report noted that the global water cycle is being disrupted and “projects with high confidence an increase in the variability of the water cycle in most regions of the world and under all emissions scenarios.” That means, in plain language, more droughts and more flooding. The report additionally projects ocean oxygen loss “substantially greater in 2080–2099 than assessed in” another IPCC special report released in 2019.

More heat, more melting in future centuries

Wish for more bad news? How about this:

“Levels of global warming … that have not been seen in millions of years could be reached by 2300, depending on the emissions pathway that is followed. For example, there is medium confidence that, by 2300, an intermediate scenario used in the report leads to global surface temperatures of 2.3°C–4.6°C higher than 1850–1900, similar to the mid-Pliocene Warm Period (2.5°C–4°C), about 3.2 million years ago, whereas the high CO2 emissions scenario SSP5-8.5 leads to temperatures of 6.6°C–14.1°C by 2300, which overlaps with the Early Eocene Climate Optimum (10°C–18°C), about 50 million years ago.” [Page TS-11]

Even if humanity were to stop producing greenhouse gas emissions today, our descendants will be faced with rising sea levels. Seas will be at least a meter higher by the end of the century, a forecast that would have to be revised upward if the amount of additional sea level rise that would occur from disintegration of marine ice shelves or faster than expected loss of ice from Greenland is included. The report states, “Although past and future global warming differ in their forcings, evidence from paleoclimate records and modelling show that ice sheet mass and global mean sea level (GMSL) responded dynamically over multiple millennia (high confidence). … Beyond 2100, GMSL will continue to rise for centuries to millennia due to continuing deep ocean heat uptake and mass loss from ice sheets, and will remain elevated for thousands of years (high confidence).” [Pages TS-14, TS-45]

The long-term forecast is for a weakening of the Gulf Stream with centuries necessary for a return to present strength. A near complete loss of Greenland ice sheet and a complete loss of West Antarctic ice sheet are projected to occur irreversibly over multiple millennia. And thus the conclusion that:

“The increase in global ocean heat content will likely continue until at least 2300 even for low-emission scenarios, and global mean sea level rise will continue to rise for centuries to millennia following cessation of emissions due to continuing deep ocean heat uptake and mass loss of the Greenland and Antarctic Ice Sheets (high confidence). … The response of biogeochemical cycles to anthropogenic perturbations can be abrupt at regional scales and irreversible on decadal to century time scales (high confidence). … Continued Amazon deforestation, combined with a warming climate, raises the probability that this ecosystem will cross a tipping point into a dry state during the 21st century (low confidence).” [Page TS-72]

Even with the uncertainty about the future of the Amazon, that clear cutting of the world’s lungs can only have a negative effect on global climate is not in dispute, however difficult it remains to determine the extent or speed of the damage.

There is plenty more material for readers with a strong stomach, but the above paints the picture clear enough.

Setting a goal but doing little to achieve the goal

Under current conditions and scenarios, it would be impossible to keep the global temperature increase below the 2-degree threshold commonly seen as the outer limit before the climate spirals beyond control and catastrophic change is likely, much less the 1.5-degree goal of the Paris Accord. According to Climate Action Tracker, an independent scientific analysis produced by the research organizations Climate Analytics and New Climate Institute, the pledges and targets set by the world’s governments, if achieved, would result in a temperature rise of 2.4 degrees by 2100. Current policies, if not altered, would result in an increase of 2.9 degrees.

Drastic reductions, well beyond what has been committed to, are necessary to attain even the 2-degree target. Two University of Washington statisticians, Peiran Liu and Adrian Raftery, in a paper published in February 2021 in the peer-reviewed journal Communications Earth & Environment, calculate that the world’s governments need to increase the rate of greenhouse gas emissions cuts by 80 percent from current levels. The authors write:

“On current trends, the probability of staying below 2 °C of warming is only 5%, but if all countries meet their nationally determined contributions and continue to reduce emissions at the same rate after 2030, it rises to 26%. If the USA alone does not meet its nationally determined contribution, it declines to 18%. To have an even chance of staying below 2 °C, the average rate of decline in emissions would need to increase from the 1% per year needed to meet the nationally determined contributions, to 1.8% per year.”

Considerably deeper reductions would be needed to attain the 1.5-degree goal, and would require “reaching close to global net zero emissions by 2045.” Even to achieve an increase of no more than 2 degrees would require a 66% reduction in emissions from 2010 to 2070. The world certainly is not on any such course.

We can’t shop our way out of global warming

It should be obvious, but unfortunately needs to be continually restated, that you can’t have infinite growth on a finite planet. The dynamics of capitalism demand that growth be ceaseless; the system can’t function without it. And given that corporations, through their stranglehold on the world’s governments, can offload their responsibilities such as damage from pollution onto society, there is little incentive for them to cut their greenhouse gas emissions or reduce their pollution of the environment. Financial markets demand ever higher profits, and will punish the stock of corporations that fail to do so. Stock prices represent expectations of future profits; if profits don’t rise, the stock price doesn’t rise, making financiers angry and thereby put pressure on executives to do as they are expected.

Every incentive in a capitalist economy is for there to be more production, and a capitalist economy that doesn’t grow also means fewer jobs. Even a small increase in gross domestic product can result in overall job loss because jobs are cut faster by cost-cutting capitalists than tepid growth in demand can create them. Moreover, even if government regulation were to make it difficult or impossible for an industry to remain solvent, capitalism doesn’t guarantee anybody a job. People don’t travel across continents to take jobs at a North Dakota oil well or an Alberta tar sands dig if there are viable alternatives back home. Corporate executives accustomed to taking home gigantic salaries aren’t eager to see their businesses wind down.

^{Haze from forest fires in St. Mary Valley, Glacier National Park in August 2015, during the hottest and driest summer in Pacific Northwest history. (photo by Pete Dolack)}

“Green capitalism” isn’t going to save us. Green capitalism is an illusion. We can’t shop our way out of global warming nor are there technological magic wands that will save us. There is no alternative to a dramatic change in the organization of the global economy and consumption patterns. Effecting such a change is impossible under capitalism. Not even a total switch to renewable energy, as laudable and necessary as such a change would be, is sufficient by itself to reverse global warming. Solar panels, wind turbines, electric vehicles and other renewable-energy infrastructure require heavy manufacturing and the use of metals and sometimes toxic rare earths to make. And a whole lot of them will have to be made.

The task of any capitalist corporation is to accumulate capital, and it must grow while meeting the rigors of competition to do so. Although greedy or immoral people are certainly not unknown in corporate boardrooms, the personality of the capitalist doesn’t particularly matter. Competition mandates corporate behavior, and the whip of the financial industry is there to enforce that behavior.

As Joel Kovel, in his classic book The Enemy of Nature put it, industrialists and financiers (those who control the economic system and thus exert decisive influence over the political system through their economic power), are structurally incapable of dealing with the environmental crisis. He wrote:

“Each society selects for the psychological types that serve its needs. It is quite possible in this way to mold a great range of characters toward a unified, class purpose. To succeed in the capitalist marketplace and rise to the top, one needs a hard, cold, calculating mentality, the ability to sell oneself, and a hefty dose of the will to power. None of these traits is at all correlated with ecological sensibility or caring, and they are induced by the same force field that shapes investment decisions. … Of course greed plays a role. How could it not when stupendous fortunes can be had for compliance with the rules of the game? But the question is how greed, or the drive for power, or cold and calculating ways of thought, lead to blindness and rigidity. These are the salient traits, and they arise from the intersection of psychological tendencies with the concrete lifeworld of the capitalists. … If you sit at the heart of the world’s financial centers, fly in private jets, manipulate billions of dollars with the tap of a keypad and control a productive apparatus capable of diverting rivers and sending missions to Mars, you are not likely to experience the humility of a St. Francis or the patient tenacity of a Rachel Carson.”

Make the future worthless so tomorrow doesn’t matter

Even standard accounting works against dealing with global warming and pollution. Capitalist economics discounts the future so much that future life is seen as nearly worthless. Thus, in this type of accounting, there is no cost for future pollution.

Authors Richard York, Brett Clark and John Bellamy Foster put this plainly in a thoughtful May 2009 article in Monthly Review. They wrote:

“Where [orthodox economists] primarily differ is not on their views of the science behind climate change but on their value assumptions about the propriety of shifting burdens to future generations. This lays bare the ideology embedded in orthodox neoclassical economics, a field which regularly presents itself as using objective, even naturalistic, methods for modeling the economy. However, past all of the equations and technical jargon, the dominant economic paradigm is built on a value system that prizes capital accumulation in the short-term, while de-valuing everything else in the present and everything altogether in the future.”

Even with a humanistic accounting regime and the needed changes to make the necessary reductions in greenhouse gas emissions, the cost of achieving the goals of averting catastrophic climate change will be high. The idea that all the new jobs created by the transition to renewable energy will somehow mean there will be no cost to the economy as promoted by many liberal environmental organizations is not credible, and it would be better to face up to that. Denying that reversing global warming will be virtually cost-free is not much more realistic than the conservative fantasy that global warming isn’t reality.

Nor should we deny the likelihood that the peoples of the advanced capitalist countries will have to consume less energy in the future. Although renewable energy will become more efficient in the future and the problem of battery energy storage will probably be reasonably solved in the not too distant future, they simply won’t provide the bang for the buck that fossil fuels provide. There is a reason those are used — they provide more energy than alternative sources. This reduction in energy usage needn’t mean trying to read by candlelight. Ending planned obsolescence, making products last much longer and becoming serious about recycling can make up a significant part of the energy gap. Humanity is using natural resources far beyond their replacement rate. Basic mathematics tells us that can’t continue indefinitely.

But what would be the cost of not seriously addressing global warming? That price will surely be vastly higher than the costs of not doing so. What price should our descendants pay if we don’t move to an economic system that values life rather than only profits, a system that produces for human and community need instead of for the profit of the one percent? That price will likely be a very high one, and our descendants are not likely to look kindly upon us for despoiling their world and leaving them with enormous problems, not least drowning cities, a chaotic climate and diminished areas for reliable agriculture. Our choice remains socialism or barbarism.

Business as usual equals many extra deaths from global warming

Is it already too late to stop global warming? That question is not asked with thoughts of throwing up hands in despair and giving up. Rather, that question must be asked in the context of mitigating future damage to whatever degree might yet be possible.

The context here is that the carbon dioxide, methane and other greenhouse gases thrown into the atmosphere don’t magically disappear but will have effects that will persist for centuries. A ton saved today is a ton saved tomorrow.

There are the mass disruptions that humanity will almost certainly see from dramatic rises in sea levels and the disruptions to agricultural patterns and sea life. Then there is the human health impact. In what its authors say is the most detailed attempt yet undertaken to quantify what the future cost of global warming will be in terms of mortality, a new scientific paper predicts the future will see significant increases in deaths.

Sixteen researchers, collaborating on a National Bureau of Economic Research paper titled “Valuing the Global Mortality Consequences of Climate Change Accounting for Adaptation Costs and Benefits,” estimate that under “business as usual” — that is, Earth’s current trend of steadily increasing greenhouse gas emissions continues — there would be 85 extra deaths per 100,000 people annually by the end of the 21st century. To put that statistic in perspective, all the world’s cancers currently are responsible for 125 deaths per 100,000 people, according to World Health Organization data. Or to be put it another way, the 85 extra deaths represent a toll comparable to the global total of deaths from infectious diseases in 2018.

Baffin Island in the Canadian arctic (photo by Doc Searls)

As would be expected, the increased deaths will be disproportionally suffered in the Global South. Although the financial cost of mitigation is predicted to be higher in the advanced capitalist countries than elsewhere, the easing of cold weather in winter months might actually cause death rates to decline in high-latitude, high-income locations. The authors put that possibility in stark terms with this comparison:

“The costs of climate change induced mortality risks are distributed unevenly around the world. Despite the gains from adaptation … there are large increases in mortality risk in the global south. For example, in Accra, Ghana, climate change is predicted to cause damages equivalent to approximately 160 additional deaths per 100,000 annually under [the business as usual scenario] in 2100. In contrast, there are gains in many impact regions in the global north, including in Oslo, Norway, where we predict that the equivalent of approximately 230 lives per 100,000 are saved annually. These changes are equal to an 18% increase in Accra’s annual mortality rate and a 28% decline in Oslo’s.”

And thus their conclusion that “Today’s poor bear a disproportionately high share of the global mortality risks of climate change, as current incomes (as well as current average temperatures) are strongly correlated with future climate change impacts.” In other words, those least responsible for global warming will pay the highest price for it.

To make these predictions, the authors gathered mortality statistics from 41 countries accounting for 55 percent of the world’s population, which they say enables them to have put together a more comprehensive analysis than previously attempted by earlier studies.

It won’t be pretty for our descendants

In a different scenario, under which greenhouse gases are stabilized in coming years, the expected number of excess deaths would be less, although still concentrated in the Global South. Under this scenario, the amount of carbon dioxide equivalent is presumed to stabilize at above 500 parts per million (ppm), and although that is far less than the “business as usual” scenario, it should be remembered that today’s carbon dioxide equivalent content is 407 ppm. And that is with the recent downward blip thanks to the pandemic. To use non-scientific terminology for what would happen in a 500 ppm world, our descendants will be screwed.

To have a hope of keeping the eventual total of global warming from the start of the Industrial Revolution to under 2 degrees Celsius, considered the outside limit before uncontrollable, catastrophic environmental disruptions are triggered, atmospheric greenhouse gases will have to be held to not much more than present-day levels and then brought down.

Without a drastic change, soon, in global output of greenhouse gases — and no such change is anywhere in sight — even the scenario of stabilizing greenhouse gases at 500 ppm seems out of reach. But even if we could suddenly convert to a carbon-neutral economy and cease adding net gains to atmospheric greenhouse gases, it may already be too late. More worrisome still, the effects of global warming are occurring faster than expected.

The Arctic is warming two to three times faster than Earth is overall. The resulting faster than expected loss of land ice contributes to a faster sea level rise and the loss of sea ice adds to global warming in a feedback loop. That’s because a dark ocean surface absorbs solar radiation up to 10 times more readily than the brighter sea ice surface. In a 2019 paper, “Radiative Heating of an Ice-Free Arctic Ocean,” published in Geophysical Research Letters, three oceanographers and atmospheric researchers calculate that if the Arctic Ocean becomes ice-free, the loss of the ice’s reflective power radiating solar energy back into space would be the equivalent to adding one trillion tons of carbon dioxide to the atmosphere. That would be roughly equal to adding 25 years of additional global CO₂ emissions.

Although an ice-free Arctic Ocean is still generally predicted to be well into the future, that future might arrive much sooner than expected. Scientists at the British Antarctic Survey, publishing this week in the journal Nature Climate Change, believe it is possible for the Arctic to be ice-free as soon as 2035, a possibility based on study of Arctic sea ice during the last interglacial period, when Arctic land summer temperatures were 4 to 5 degrees C. higher than the pre-industrial baseline. By one measure, current temperatures above 60 degrees north latitude have already risen about 3 degrees C. since 1900.

There’s plenty of bad news to go around

As it is, predictions of what the world will look like are increasingly dire. For example, a 2015 paper by nine scientists led by geologist Andrea Dutton at the University of Florida published in the journal Science found that when global temperatures in the past were between 1 and 2 degrees C. above the pre-industrial base temperature, sea levels rose six to nine meters. What that finding means is that humanity may have already committed itself to an eventual sea level rise of that magnitude.

Need more? A 2016 paper published in Atmospheric Chemistry and Physics, authored by 19 climate scientists from the United States, France, Germany and China and led by James Hansen, predicts that the melted freshwater from melting glaciers will add to the other scenarios to create a feedback loop that could culminate in a sea level rise of “several meters” in 50 to 150 years.

Still another paper, “Explaining Ocean Warming: Causes, Effects and Consequences,” concludes that the mean global ocean temperature will increase by as much as 4 degrees C. by 2100. This 2016 paper states that Earth has tipped into a heat imbalance since 1970, and this excess heating has thus far been greatly ameliorated because the world’s oceans have absorbed 93 percent of the enhanced heating since the 1970s. This accumulated heat is not permanently stored, but can be released back into the atmosphere, potentially providing significant feedback that would accelerate global warming. Dozens of climate scientists from around the world contributed peer-reviewed work to this report, research that in turn is based on more than 500 peer-reviews papers.

There is plenty more, but perhaps the foregoing is sufficient. And so what is the world doing? Very little. The December 2019 meeting of the Conference of the Parties to the United Nations Framework Convention on Climate Change (COP 25) in Madrid concluded with the world’s governments saying the conference “Notes with concern the state of the global climate system” and “Decides to hold, at its twenty-sixth (2020) and twenty-seventh (2021) sessions, round tables among Parties and non-Party stakeholders on pre-2020 implementation and ambition.” The time for “noting” there may be a problem would seem to be well past. A year earlier, at COP24 in Katowice, Poland, the world’s governments agreed to a rulebook with no real enforcement mechanism. And at COP23 in Bonn, participants congratulated themselves for their willingness to talk and agreed they would talk some more.

And so it goes, as Kurt Vonnegut liked to say. We are fortunate that hot air from political leaders doesn’t add to global warming, however weighed down they are by the piles of corporate money that keep “solutions” at the level of talking rather than action. Our descendants are not likely to be amused.